Summary

Concrete experiences are key for people to relate to numbers and understand foundational mathematical concepts. In particular, they allow children to interact much sooner in their life with mathematics and use it to learn about the World.
A good feeling emerges from such experiences, when something new is learnt. As a consequence, a flywheel is created for lifelong development.

The Beauty of Numbers (Mathematics)

A long time ago, when I was in University, I unfortunately experienced many times how some of my dear colleagues were struggling with mathematics - they could not understand the intuition behind the numbers. This led to memorising things to pass a test and no real learning…. I helped them on many occasions, but afterwards I often wondered, what was blocking their ability to see the “picture” behind an equation and understand the beauty of mathematics.
What is this beauty one might ask? In my mind, mathematics is a tool to create an abstract model of the World. If we understand the model and how it applies to concrete applications, we learn not only how to think about the World, but more importantly, how we can make it a better place for our children and future generations. I find it fascinating that mankind’s progress is built on numbers: without it there would be no advancement.
Fast forward to today and my son Santiago will soon turn four. I often think about his education and ask the same question: what can I do to help him see the “picture” behind numbers? I am hoping the below will help me to support him in this journey.

Deep Time Walk

I recently came across a podcast called Long Time Academy (I highly recommended it, in particular the point about thinking about future generations in today’s decisions), where they discussed an experience called Deep Time Walk. In it, they explain how Earth is 4,600 million years old and how from this long time perspective, the last 100 years are just a blink of an eye (they equate to 0.00000002% of all time elapsed so far). Furthermore, they mention how people struggle to relate to 0.00000002% if they are simply told the figure.

Figure 1: Earth is 4.6 billion years old.

The podcast then suggests going for a walk of 4,600 metres.

Figure 2: 1 metre = 1 million years.

On average it will take about one hour to do the walk, which means the last metre takes approximately ONE second to cover, with ONE step. But that very last step equals the last one million years, a tiny bit of the step (10cm) equates to 100,000 years and a very, very tiny bit of the step (1cm) equates to 1,000 years.
This then makes the last 100 years (the 0.00000002%) a very concrete experience that people can relate to, and understand how short 100 years are, in the grand scheme of things (and how quickly we are damaging the World for future generations...).
My next thought was that this experience works for both adults and children. I was wondering if there were other “experiences” out there similar to this one?

Maria Montessori

In the second step in my journey, I randomly found in a bookstore, Maria Montessori’s book. In it, the famous author describes how through using their hands, children aged 3-6 years learned how to write words as they picked up wooden letters and how they tried to figure out what (A+B+C)³ equates to by using wooden tri-dimensional blocks. I was blown away when I read this in a book about children that are now 80+ years old.
Once again, I was seeing the concept of using a concrete experience to learn about letters and numbers, as a foundation to build upon, in order to be able to develop abstract thinking. It was wonderful.
I have not tested it yet with my son, but both examples made it very clear that the best way to see the “picture” behind an equation and understand the beauty of mathematics, is through the use of concrete experiences.

A plus B square

Finally, I decided to give it a go at deriving (A+B)² in a way that I can use to teach my son in the near future (or using Montessori's approach, to help him learn by himself...). If you also have children please do keep reading.

Step 1: Cut a square from piece of paper and colour it in blue.
Figure 3: Area of a blue square.
Step 2: Cut a square from a piece of paper with a different dimension and colour it in red.
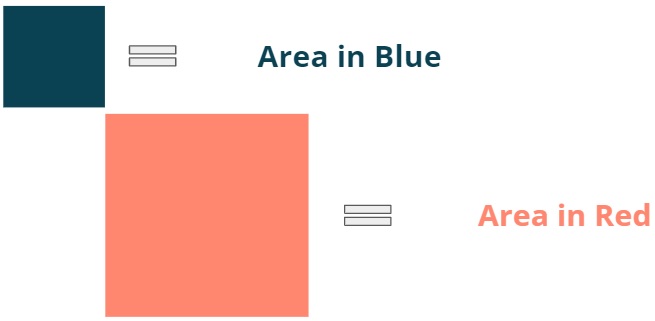Figure 4: Area of a red square.
Step 3: Cut a rectangle with one dimension matching the side of red square and the other dimension matching the side of blue square. Colour it in green.
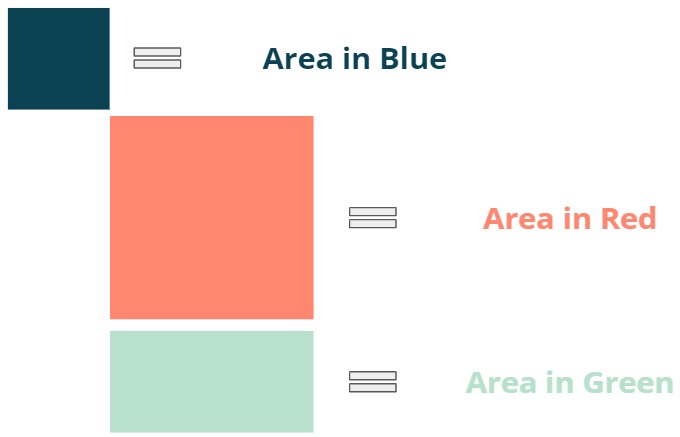Figure 5: Area of first green rectangle.
Step 4: Repeat step 3.
Figure 6: Area of second rectangle.
Step 5: Organise all the pieces together in a square.
Figure 7: Pieces organised in a square.
Step 6: Cut a new grey square with the same area and put it side by side with the other square.
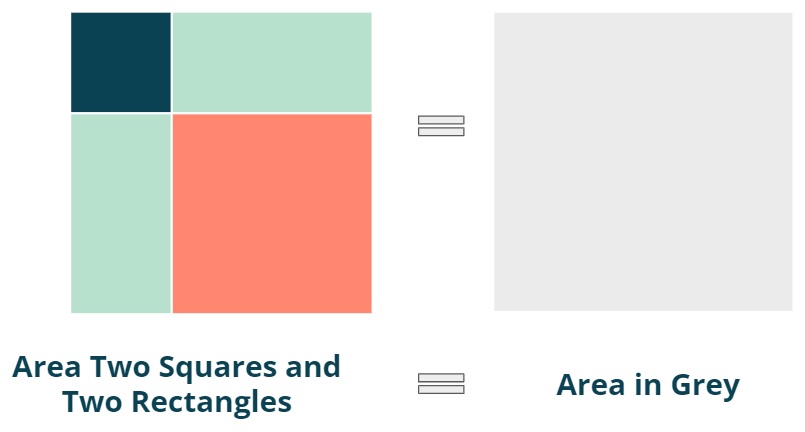Figure 8: Pieces organised in a square.
This is where the magic happens. For small children who have not learned numbers yet, they can have a concrete experience of what (A+B)² means. For older children (and adults) one can then use this experience to see the “picture” behind an equation.
Step 7: Assign letters to each side of the squares and rectangles.
Figure 9: Area in grey equals area of the four components.
Final step: use the concrete experience to see the “picture” behind the abstraction for (A+B)² . Beautiful!
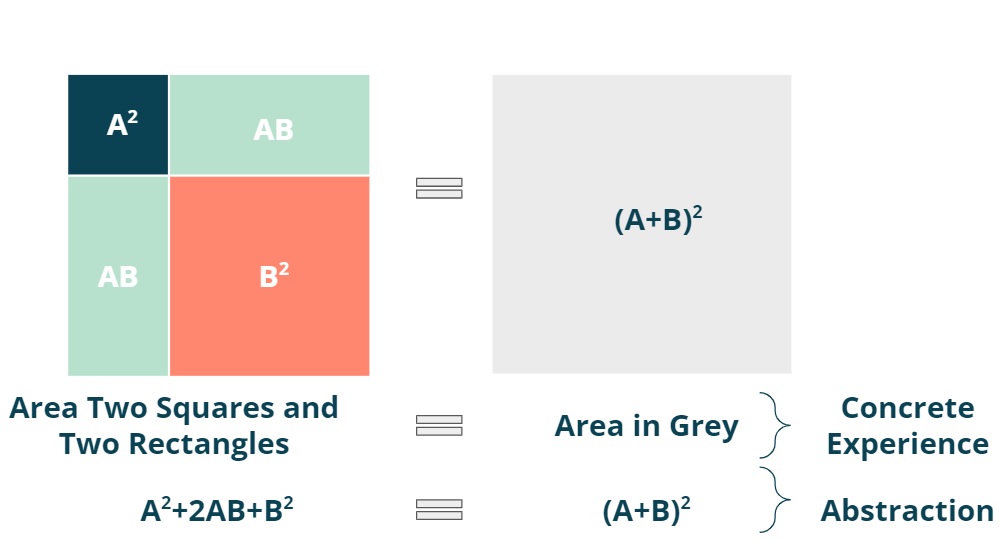Figure 10: (A+B)².

Conclusion - A flywheel for lifelong development

Why do kids love chocolate and always want more? From a neurological point of view, the brain is hit with a chemical called dopamine, which gives them a feeling of happiness and pleasure, that they want to repeat over and over again. The same thing happens, when someone finally achieves a hard goal or completes a difficult task.
Going through these types of concrete experiences is a similar process: it creates a feeling of happiness (dopamine…) when you finally understand it. It then induces a person, to seek other concrete learning experiences, like the ones they just had. Learning becomes fun and a flywheel is created for lifelong development.

If you require support or have any questions my contact is:

Appendix - What about having a go at figuring out (A+B+C)²?

If you found the prior example interesting and easy to understand, the below should be very fun to learn (and dopamine inducing… at least for me).

Step 1: Using the prior concrete experience induces real learning that can be used to tackle this problem.
Figure 11: Recursive learning.
Step 2: Divide the two rectangles for C(A+B) into four rectangles.
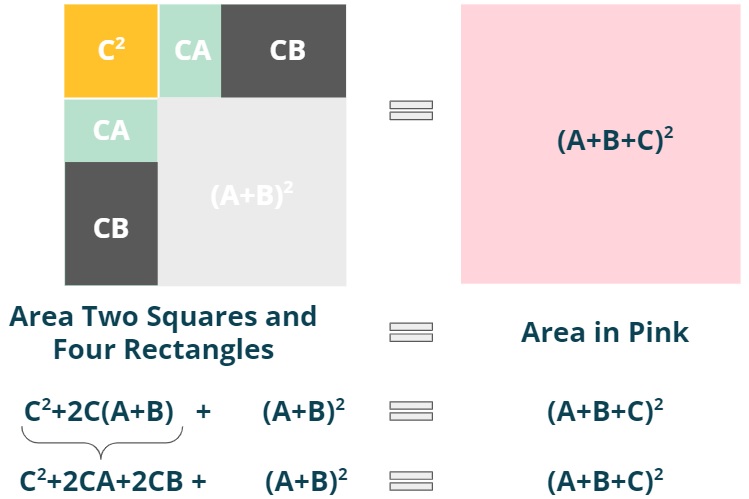Figure 12: Step 2.
Step 3: Divide the grey square into two squares and two rectangles.
Figure 13: Step 3.
Final step: Problem solved.
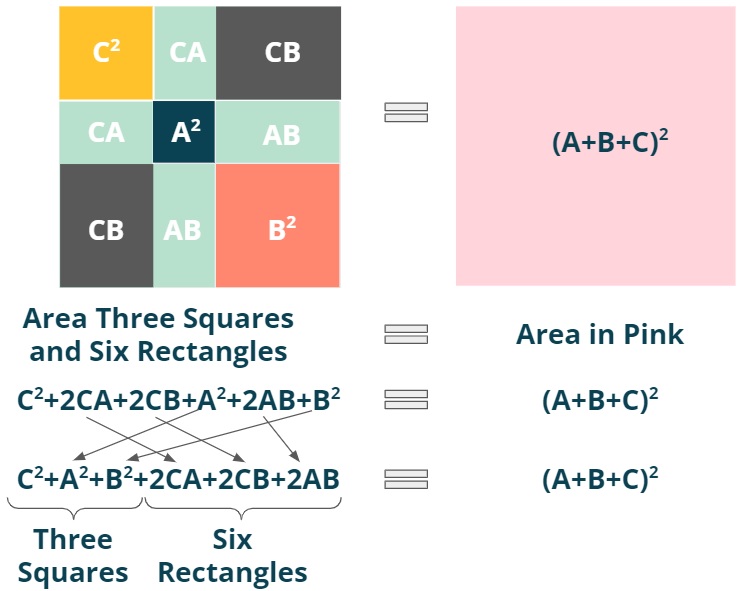Figure 14: Final step.